#数学 エドワード・フレンケルさんの数学ミステリー白熱教室の第2回 https://www.youtube.com/watch?v=8S-5eh1AMA4 … ではガロア理論の話が出て来るのですが、解の対称性の一般の3次と4次方程式の場合に関する解説は→https://twitter.com/genkuroki/status/667978073397047296 …
@genkuroki #数学 一般の3次方程式の解法は因数分解 x^3+y^3+z^3-3xyz=(x+y+z)(x+ωy+ω^2z)(x+ω^2y+ωz)、ω^2+ω+1=0から簡単に得られ、4次方程式でも同様。この2つは対称性を理解するためにはとてもよい例になっています。
@genkuroki #数学 終わりましたね。フレンケルさんが例として使ったy^2+y=x^3-x^2は楕円曲線の方程式です。それに対応するモジュラー形式はη(q)^2 η(q^{11})^2 でした。他の例については→https://twitter.com/genkuroki/status/667513513573675009 …
@genkuroki #数学https://www.math.kyoto-u.ac.jp/~tetsushi/files/msj200903_slide …伊藤哲史、佐藤・テイト予想の解決と展望、2006ラングランズプログラムに興味を持った人はSato-Tate予想=佐藤sin^2予想についてもググると楽しめると思います。今世紀の成果。
#数学 http://www.nhk.or.jp/hakunetsu/math/ E.フレンケルさんの数学ミステリー白熱教室関連の私の発言は http://twilog.org/genkuroki/hashtags-数学 … およびそのちょっとしたリンク先(間違って #掛算 タグを付けた分)でまとめ読みできます。
#数学 Edward Frenkel on Eichler's reciprocity lawhttp://m759.net/wordpress/?p=39889 …フレンケルさんが例として使った y^2+y=x^3-x^2 と (η(q)η(q^{11}))^2 のあいだの有名な対応に関する覚書

#数学 http://www.fen.bilkent.edu.tr/~franz/ta/tate.pdf …J.T.Tate, The arithmetic of elliptic curves, Invent.math.1974のp.200にフレンケルさんが使った例が載っている。pic.twitter.com/hU1RmTTyjx
#数学 E.フレンケルさんが数学ミステリー白熱教室の第3回で説明用に使った「y^2+y=x^3-x^2」は各種解説で本当によく使われている楕円曲線の例で、数学を少し勉強したことがある人にとっては「いつものあれ」という感じのものです。
#数学 コンピューターに慣れている人であれば、フレンケルさんが紹介していた神秘的な結果を自分で計算して確認できると思います。(1)各素数pについて、y^2+y=x^3-x^2の両辺をpで割った余りが等しくなるようなx,y=0,1,..,p-1の組全体の個数S(p)を求める。続く
#数学 続き(2) q×((1-q)^2(1-q^2)^2(1-q^3)^2…)×((1-q^{11})^2(1-q^{22})^2(1-q^{33})^3…)を展開して q^n の係数 a_n を求める。(3) p-S(p)=a_p となることを確認する。続く
#数学 続き。楕円曲線 y^2+y=x^3-x^2 について以上の結果はアイヒラーさんが1954年に証明し、志村五郎さんによって一般化されました。 http://projecteuclid.org/euclid.jmsj/1261153636 …
#数学 続き。Dedekindのeta函数がη(q)=q^{1/24}(1-q)(1-q^2)(1-q^3)…によって定義されます(|q|<1)。この函数を使えばフレンケルさんの話に出て来た函数は f(q)=(η(q)η(q^{11})^2 と書けます。
#数学 続き。その f(q) は q=exp(2πiτ) (τは複素上半平面の点)とおくとき、ad-bc=1を満たす整数a.b,c,dによるτ→(aτ+b)/(cτ+d) という一次分数変換である因子倍を除いて変わらないという特別な性質を持っています。続く
#数学 続き。複素上半平面上への離散群SL(2,Z)の作用の様子を、複素上半平面を単位円盤上に一対一に写して理解するためのゲームが http://tsujimotter.info/works/fundamental-domain/disk.html … にあります。(SLとPSLの違いは気にする必要がない) 続く
#数学 続き。一方、各素数pごとにpで割った余りの世界で楕円曲線の点の個数を数える話は、任意の整数xが「x^pとxをpで割った余りは等しい」という対称性を持っている話と関係があります。続く
#数学 「ad-bc=1をみたす整数a,b,c,dによる一次分数変換の対称性」(PSL(2,Z)作用)と「p乗してもpで割った余りは不変であるという対称性」(フロベニウス作用)は全然別の世界に住む対称性だという点が、数学の世界がどれだけ神秘的であるかを理解するためには重要です。
#数学 PSL(2,Z)作用は実はもっと巨大な対称性(代数群のアデール)の一部分だとみなせ、フロベニウス作用はガロア群サイドの対称性だとみなせます。これらの全然違う世界が実はある意味で同じになっているのではないかということが20世紀のあいだにわかって来たのです。
#数学 そして、そういう神秘的な関係に、楕円曲線y^2+y=x^3-x^2の素数位数の有限体上での点の数(ガロアワールドの住人)と保型形式f(q)=(η(q)η(q^{11})^2の展開の係数(保型ワールドの住人)を実際に自分で計算して比較すれば誰でも触れることができるわけ。
#数学 続き。フレンケルさんが「志村・谷山・ヴェイユ予想」と呼んでいた予想(他にも色々な呼び方があるらしい)は「任意の有理数体上の楕円曲線に対して先に挙げたような意味で対応する保型形式が存在する」という予想のことです。続く
#数学 続き。その予想は現在では、ガロアワールドと保型ワールドのあいだの関係に関する巨大な予想集に発展しています。これが所謂「ラングランズ・プログラム」の話です。続く
#数学 続き。そういう一般人にとって内容の詳細がさっぱりわからない「単なるお話」ではなく、自力で計算することによって、数学の世界のさらなる深みを確認できる話があります。それはSato-Tate予想=佐藤sin^2予想。佐藤幹夫さんは計算機でたくさん計算して予想を立てました。続く
#数学 続き。特別に数学の訓練を受けていない人であっても、佐藤sin^2予想を打ち立てるために実行されたコンピューターによる計算を自力で再現できます。計算法は http://www2.tsuda.ac.jp/suukeiken/math/suugakushi/sympo16/16_8nanba.pdf … で難波完爾さんが詳しく説明しています。続く
#数学 (η(q)η(q^{11}))^2には楕円曲線y^2+y=x^3-x^2が対応していた。 http://www2.tsuda.ac.jp/suukeiken/math/suugakushi/sympo16/16_8nanba.pdf … によれば(η(q)η(q^5))^2にはy^2=x(x^2+x+1)が対応するらしいのでそちらも確認してみると面白いと思います。
#数学 フレンケルさんが例に使ったのと同じ楕円曲線y^2+y=x^3-x^2を例に用いたSato-Tate予想に関する解説が、黒川信重「佐藤-テイト予想の歴史」数学のたのしみ2008最終号pp.23-34にあります。 http://www.amazon.co.jp/dp/4535603235
#数学 Sato-Tate予想について例で説明します。素数位数pの有限体をF_pと書きます。フレンケルさんは楕円曲線の方程式y^2+y=x^3-x^2のF_pでの解(x,y)全体の個数をS(p)と書いていました。各素数pごとにS(p)をコンピューターで求めることができます。続く
#数学 続く。アイヒラーさんの証明によって、a_p=p-S(p)は保型形式(η(q)η(q^{11}))^2の展開のq^pの係数としても計算できるのでした(コンピューターで計算するときにはこちらの方法を使った方が圧倒的に楽)。続く。
#数学 続き。おおざっぱには、楕円曲線の方程式y^2+y=x^3-x^2のF_pでの解全体の個数は「p個±誤差」になっていると考えられます。なぜならば、F_pの元の組(x,y)全体の個数はp^2個あり、方程式が1本あるので点の個数は大体1/pに減るはずだからだ。続く
#数学 続き。実際には方程式が非線形で複雑なので、ぴったり1/pにはならず、期待値からのずれが生じる。だからa_pの絶対値は|a_p|=|p-S(p)|=(予想される解の個数の期待値と実際の解の個数の違い)=(期待値からのずれ)と解釈されます。続く
#数学 続き。解の個数の期待値からのずれ|a_p|はハッセによって |a_p|<2√p を満たすことが知られています。期待値からのずれに平方根が出て来ることはギャンブル(統計学)をやっている人にはお馴染みの現象なのですが、ヴェイユさんがどこかでそういうことを言っていたと思う。続く
#数学 続き。不等式 |a_p|<2√p は後にヴェイユさんによって一般化され、有限体上の任意の多様体でも同様のことが成立していると予想されました。これは有名なリーマン予想の有限体上の多様体バージョンになっています。続く
#数学 続き。a_p の分布については不等式 |a_p|<2√p 以上のことが知られています。それが次のSato-Tate sin^2予想です:a_p=2√p cos θ (0<θ<π)と書くとき、素数pの個数を増やすときθの分布関数は(sin θ)^2の定数倍に収束する。
#数学 続き。ただし、楕円曲線が特別な対称性を持たない(虚数乗法を持たない)と仮定しておかなければいけません(その仮定が成立しない楕円曲線は例外的)。楕円曲線の有限体F_pでの点の個数の期待値からのずれの分布函数が分かるというのは実は数学的に極めて深い結果。続く
#数学 続き。もしかしたら、コンピューターが得意なアマチュア数学者が新しくて深い数論的予想を発見するというようなことがこれからあるかもしれませんね。数学に詳しい人が増えれば、コンピューターが身近になっているのできっとそういうことが起こると思う。
#数学 E.フレンケルさんの数学ミステリー白熱教室関連の私のツイートは http://twilog.org/genkuroki/hashtags-数学 … でまとめて読めます。
#数学 http://twilog.org/genkuroki/hashtags-数学 …自分の手を動かしたり、コンピューターをぶんまわしたりして、自力で遊べるE.フレンケルさんの数学ミステリー白熱教室関連の話題を集めたつもり。数学は話を聞くだけだと本当の所はよくわからず、何かを自分でやってみた方が楽しいと思う。
#掛算 続き。言い忘れていましたが、佐藤・テイト予想もラングランズ哲学の範疇で証明されました。ラングランズ哲学的に佐藤・テイト予想はフェルマー予想よりも一段深い場所に位置付けられ、そこまで数学は進んだということです。続く
#掛算 続き。y^2+y=x^3-x^2のような「いつものあれ」を使えば、リーマン予想の有限体上での類似、佐藤・テイト予想、楕円曲線と保型形式の対応などなどに関する数値計算を誰でもできますね(コンピューターを使わないと大変だろうけど)。そういうブログ記事が現れると信じたい。続く
#掛算 続き。ブログの類で数式を見せるにはMathJaxが便利です。LaTeX方式で数式を「普通に」書けばそのままブラウザで数式が表示されるようになります。私が数年前に書いたMathJaxの解説→ http://genkuroki.web.fc2.com/
#数学 「数学ミステリー白熱教室」をGoogleで動画検索https://www.google.co.jp/search?q=�%95�学ミステリー白熱教室&tbm=vid …反応を検索してチェックすると、講師のエドワード・フレンケルさんが大人気ですね。わからなくても面白いという反応も多い!
#数学 E.フレンケルさんの数学ミステリー白熱教室 http://www.nhk.or.jp/hakunetsu/math/ は4回中3回がすでに放送され、残り1回になってしまいましたね。来週の金曜日に放送されます。最終回にラングランズ・プログラムと理論物理の数学との関係について話すらしい。
#数学 ラングランズ・プログラムと理論物理の数学との関係の探求はE.フレンケルさんのガチ専門そのものなので、今まで以上に熱のこもった講義になることが期待されます。放送が終った第1~3回目を見逃した人であっても来週金曜日12/4の午後11時からの放送はチェックした方がいいかも。
#数学 E.フレンケルさんの数学ミステリー白熱教室の第1~3回の詳しい紹介を http://sci.tea-nifty.com/blog/2015/11/nhk-1127-41d4.html … に見付けた。内容を知りたい人は以下の検索も参照https://www.google.co.jp/search?q=�%95�学ミステリー白熱教室 第3回+15+11+27+動画 …https://www.youtube.com/results?search_query=数学ミステリー白熱教室 …
@genkuroki #数学 ラングランズ・プログラムのGL_1の場合(すなわち類対論)の話をしようと思ったのだが、大変そうなのでその一部分である平方剰余の相互法則の話をしようと思ったのだが、さらに話を簡単にして素数分の1の小数展開の話をする。続く
@genkuroki #数学 用意して欲しいのは、必要な精度で小数を計算してくれるソフトです。たとえばMaximaは無料で使える数式処理ソフトで結構便利です。以下の作業を実際にやってみた人は算数レベルの計算で数の世界で不思議な現象が起こっていることを確認できます。続く
@genkuroki #数学1. まず素数表を用意します2. 次に7以上の素数pに対して1/pの小数展開を小数点以下第p桁目より少し先まで計算して表にします。3. すべて循環小数になり、循環節の長さはp-1の約数になっていることもわかる。(フェルマーの小定理の応用)続く
@genkuroki #数学4. 循環節の長さが偶数のとき、その前半と後半を足すと999…9になる。たとえば、1/7の循環節は142857で142+857=999となる。1/11の循環節は09で0+9=9となる。1/13の循環節は076923で076+923=999となる。
@genkuroki #数学5. 1/pの小数点以下第(p-1)/2+1桁目の数字をマルで囲む。6. p=7を除いてマルで囲まれた数字は0または9のどちらかになる。7. マルで囲んだ数字が0と9のどちらになるかはpを40で割った余りで決まることが確かめられる。続く
@genkuroki #数学 平方剰余の相互法則というとてもキュートな数論の結果から7の結果が導かれます。マルで囲んだ数字が0になるのはpを40で割った余りが1,3,9,13,27,31,37,39のときで、9になるのは7,11,17,19,21,23,29,33のときです。
@genkuroki #数学 素数pに対する1/pの小数展開という算数レベルの話の中に平方剰余の相互法則というキュートな結果がびょこっぴょこっとかわいく顔を出している感じです。
@genkuroki #数学 平方剰余の相互法則は類対論に一般化され、類対論の非可換な場合への一般化がラングランズ・プログラムです。数論の話の良いところは算数レベルの話の中にも深い数学に繋がる現象が垣間見えていることを、誰でもたくさん計算すれば確かめられることです。
#数学 今週の金曜日に放送のE.フレンケルさんの授業はラングランズ・プログラムと理論物理の数学の関係の話になるはずなのですが、一体どうするつもりなのかとても楽しみです。今までの話題は算数からせいぜい高校1年生レベルの数学を知っていれば計算を楽しめる話でした。続く
#数学 続き。数論の話題は深い話題であっても、現象として見えている部分の解説の多くは算数の範囲内で処理できる計算ですむものがものすごく多い。実際には高校1年生レベルの数学は必要でしょうが、せいぜいそのレベルの数学を知っているだけで「何が起こっているか」を直接見ることができる。続く
#数学 続き。それに対して理論物理の場の理論の数学だと「何を見せるか」が大問題になると思う。今週の金曜日の午後11時から放送されるフレンケルさんの数学ミステリー白熱教室の第4回目(最終回)が楽しみです。毎回独立に見れも面白い話になっているのでこの回だけでも見る価値があります。続く
#数学 続き。第3回目のフレンケルさんの話には出て来なかった話題なのですが、物理サイドではなく、数論サイドでのラングランズ・プログラムの進展に興味がある人は、フェルマー予想や谷山・志村・ヴェイユ予想だけではなく、佐藤・テイト予想(sin^2予想)についも調べた方がよいと思う。続く
#数学 続き。その理由は2つ。1つ目は谷山・志村・ヴェイユ予想の解決のためにワイルズさんとテイラーさんによって開発された方法がそのまま佐藤・テイト予想の解決でも使われているという21世紀の数学の発展の流れに沿っていること。2つ目は佐藤・テイト予想も数値計算で遊べることです。続く
#数学 続き。フレンケルさんが数学ミステリー白熱教室第3回目で使った「いつもあれ」である楕円曲線y^2+y=x^3-x^2はそのまま佐藤・テイト予想の解説でも使えます。フレンケルさんの講義を聴いていれば誰でも佐藤・テイト予想の数値的確認で遊べます。続く
#数学 続き。『数学のたのしみ2008最終号』は「佐藤-テイト予想の解決と展望」特集号なのですが、黒川信重さんも伊藤哲史さんもリチャード・テイラーさんもエドワード・フレンケルさんと同じy^2+y=x^3-x^2を例に用いて解説を書いています。まさに「いつものあれ」という感じ。続く
#数学 続き。『数学のたのしみ2008最終号』は http://www.amazon.co.jp/dp/4535603235 でまだ購入できます。フレンケルさんの授業の第3回目を視聴して、さらにその先にあるものを見てみたいと思った人にはおすすめ。続く
#数学 続き。「証明」となると滅茶苦茶大変過ぎるのですが、y^2+y=x^3-x^2のような「いつものあれ」な例について様々な数値を計算して数学の世界で何が起こっているかを見て確認することであれば、算数レベルの計算をコンピューターで実行すれば誰にでも可能です。つ
#数学 続き。私による佐藤・テイト予想の解説連ツイは→ https://twitter.com/genkuroki/status/670508446849060864 …佐藤幹夫さんが計算機による計算から予想を発見した経緯については計算を実行した難波完爾さんの解説が次の場所にあります→ http://www2.tsuda.ac.jp/suukeiken/math/suugakushi/sympo16/16_8nanba.pdf …
#数学 難波さんの http://www2.tsuda.ac.jp/suukeiken/math/suugakushi/sympo16/16_8nanba.pdf … を見れば帰納的に数学の世界を調べるという数学研究のナマの様子がわかります。複素根のプロットのためにアルバイトで佐藤幹夫先生に雇われた2人の学生は数学史に名を残すチャンスを逃している(pp.102-103)。続く
#数学 続き。もしもバイトの学生2人が複素根のプロット作業を最後までやり遂げてさらにそれがどのような分布になっているかを見抜いて「佐藤先生!すべてがsin^2分布になっています!」と報告していたら、現在、佐藤・テイト予想と呼ばれている予想が別の名前になっていたかもしれない。続く
#数学 続き。難波完爾さんによる計算の貢献がどのくらいであったかについては http://www2.tsuda.ac.jp/suukeiken/math/suugakushi/sympo16/16_8nanba.pdf … を見ればわかります。そこには佐藤幹夫さんから「難波完二」さん宛の手紙の画像も載っています(p.114)。名前間違っているし。これがナマの数学史。
#数学 続き。昔の人達の「コンピューターへの飢え」は最近の人達には想像できないと思う。コンピューターは人類が開発した最高のおもちゃの一つなのですが、昔はそのおもちゃを使い放題の立場に立つこと自体が大変だった。その世代の人達は年寄になっても飢えた感覚を忘れていないように見える。
#数学 佐藤・テイト予想に現われる0≦θ≦πでの確率分布 (2/π) (sin θ)^2 dθ は3次元球面x^2+y^2+u^2+v^2=1で x=cos θ とおいたときにθをdθだけ微小に動かしたときに得られる面積(を球面全体の面積で割った値)です(図を描け!)。続く
#数学 3次元球面x^2+y^2+u^2+v^2=1の点に対して、z=x+iy,w=u+ivとおき(1,1),(2,1),(1,2),(2,2)成分をそれぞれz,w,-(wの複素共役),(zの複素共役)と定めてできる2×2の複素行列全体の集合はSU(2)という名の群になります。
#数学 これによって群SU(2)は3次元球面と同一視できます。3次元球面x^2+y^2+u^2+v^2=1(x,y,u,vは実数)の「3次元」は「表面が3次元」という意味で、中身も考えたx^2+y^2+u^2+v^2≦1は4次元の物体になります。だから想像にし難い。続く
#数学 3次元の球体x^2+y^2+u^2≦1の表面が2次元の球面になるのと同じように、4次元の球体x^2+y^2+u^2+v^2≦1の表面が3次元の球面になると考えてよいです。3次元球面は我々が日常生活でよく見る2次元球面と違って自然に群になっているとみなせる所がすごい。
#数学 3次元球面の群SU(2)は実は実3次元空間の回転群SO(3)をさらに深くとらえたものであることが分かっています。電子のスピンは通常の3次元空間の回転群SO(3)では記述できず、SU(2)を使わないと理解できない。通常の3次元空間の回転を表現するためにもSU(2)は便利。
#数学 3次元球面の群SU(2)はハミルトンの四元数を用いた実現も持ちます。3次元球面上の点に対応する四元数x+iy+ju+kv全体の集合を考えても同一の群が得られます。3次元空間の回転を扱っている文献の多くで3次元球面の群が使われています。SU(2)に関する数学的教養は大事。
#数学 1次元の円周x^2+y^2=1上の点に対応する複素数z=x+iyの掛算が複素平面の回転になっていることは高校で習います。3次元球面の点に対応する複素2×2行列(または四元数)によって3次元空間の回転を記述できることはその拡張になっているともみなせます。
#数学 3次元の回転の記述は、ゲームプログラミングで基本的なだけではなく、人工衛星の制御などにも必要なことです。本屋で立ち読みした人工衛星の本では本質的に3次元球面の群SU(2)が使われていました。そういう群の話が佐藤・テイト予想のsin^2分布の起源になっているわけ。
#数学 ある仕組みで各素数pごとに群SU(2)の共役類C_pが決まる仕組みがあって、C_p達の分布の仕方が3次元球面上への引き戻しで見たときの一様分布に対応していれば、自然にsin^2分布が出て来るわけです。
#数学 線形代数。SU(2)の共役類はSU(2)の元の特性多項式と一対一に対応しています。SU(2)の元の行列式は定義より1なので、特性多項式はトレースだけで決まることになる。SU(2)の元のトレースはその2つの固有値exp(±iθ)の実部x=cos θの2倍になります。続く
#数学 続き。-1≦x≦1に対してxをdxだけ微小に動かすときできる3次元球面x^2+y^2+u^2+v^2=1上の領域の微小面積は(半径√(1-x^2)の2次元球面の面積のdx/√(1-x^2)倍)=4π√(1-x^2) dx になることがわかります。続く
#数学 続き。4π√(1-x^2) dx を-1≦x≦1で積分すれば単位3次元球面の面積が得られるはずなのですが、√(1-x^2) dxの積分は単位円盤の上半分の面積π/2なので、結果は2π^2になります。これが正しい結果であることは別の方法でも確認できます。続く
#数学 続き。2つ前のツイートの4π√(1-x^2) dxを出す計算の途中でdx/√(1-x^2)倍が出て来る理由は高校数学IIIで習う経路の長さを積分で表わす公式を導くための考え方を使えば出ます。高校数学IIIまで習っていて基本的考え方を習得していれば大抵のことで困らない。続く
#数学 4π√(1-x^2) dxの全体での積分結果が1になるように正規化するためには3次元球面の面積(体積)の2π^2で割って (π/2)√(1-x^2) dx を考えることになります。x=cos θで変数変換すれば sin^2 分布が得られます。
#数学 4次元空間内の3次元球面x^2+y^2+u^2+v^2上に一様に分布している点列が与えられていれば、その点列をx座標に射影した結果の分布はsin^2分布になります。佐藤・テイト予想は虚数乗法を持たない楕円曲線からこのような状況が自然に得られることを意味しています。
#数学 y^2+y=x^3-x^2の場合の佐藤・テイト予想の数値的確認の手続きは以下の通り。(1)楕円曲線の方程式y^2+y=x^3-x^2の解(x,y)の素数位数pの有限体F_pでの解の個数S(p)を数えて、p-S(p)の表を作成する。続く
#数学 続き(2)η(q)=q^{1/24}(1-q)(1-q^2)(1-q^3)…とおく。(η(q)η(q^{11}))^2をqについて展開し、p次の係数をa_pの表を作る。(3)a_p=p-S(p)が成立していることを確認できる。ここまではフレンケルさんの講義の話。続く
#数学 続き。(3)までの結果はアイヒラーさんの結果。(4) |a_p|<2√pの成立を確認できる。これはハッセさんの結果。リーマン予想の有限体上での類似。(5) a_p=2√p cos θ_p, 0<θ_p<πでθ_pを定める。続く
#数学 続き(6) 0からπのあいだを適当に分割して、θ_pがどこに入るかを調べて個数を数えて、グラフにする。(7) sin^2のグラフでよく近似されているように見える! これが佐藤・テイト予想の数値確認の手続きです。どのステップも明瞭。続く
#数学 続き実際今から50年前に佐藤幹夫さん・難波完爾さんたちは以上のような計算を実際に実行して、佐藤sin^2予想が発見されることになったわけです。詳しくは→ http://www2.tsuda.ac.jp/suukeiken/math/suugakushi/sympo16/16_8nanba.pdf … (これを見れば他の例の計算の仕方もわかる)

#数学 『数学のたのしみ2008最終号』の立ち読み1楕円曲線y^2+y=x^3-x^2で保型形式との対応とハッセの定理(リーマン予想の有限体上での類似)の数値的確認。pic.twitter.com/s3oCjBHw9j
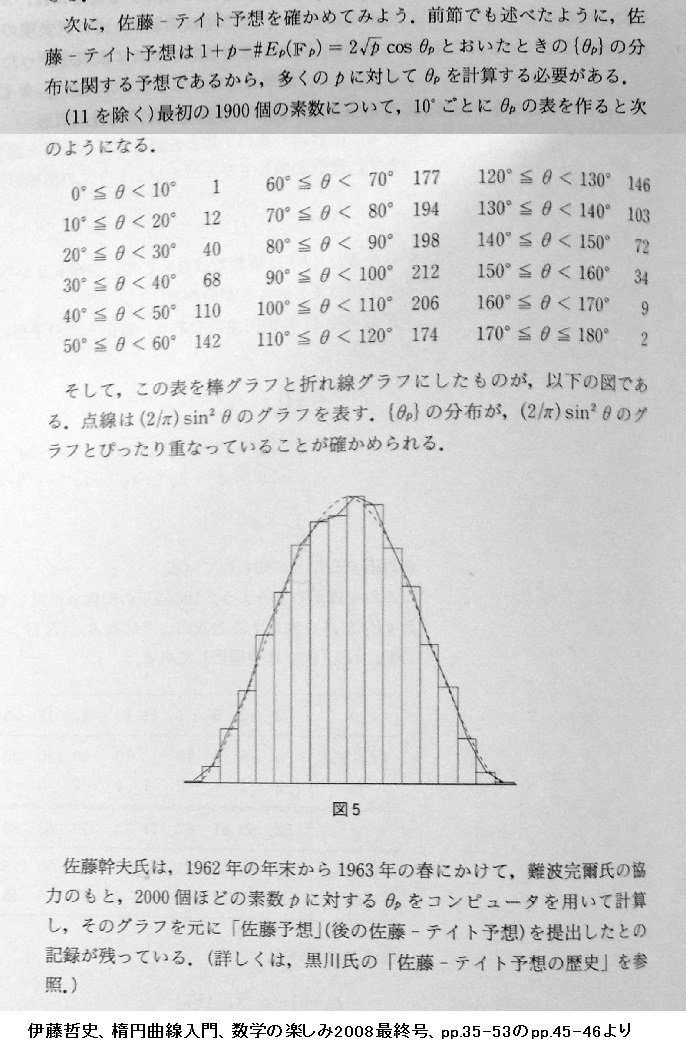
#数学 『数学のたのしみ2008最終号』の立ち読み2楕円曲線y^2+y=x^3-x^2で佐藤・テイト予想を数値的に確認。この楕円曲線はE.フレンケルさんの数学ミステリー白熱教室の第3回目でも使われています。「いつものあれ」!pic.twitter.com/ktJs62yWSv
@genkuroki #数学https://www.youtube.com/watch?v=cMi-QKmaY4E …数学ミステリー白熱教室第3回目楕円曲線 y^2+y=x^3-x^2 を例に楕円曲線に保型形式が対応するという「志村・谷山・ヴェイユ予想」について解説。フェルマー予想はその帰結。
@genkuroki #数学 続き。フレンケルさんが最後に触れている1955年に日本で開催された数論の研究集会の情報は https://www.jstage.jst.go.jp/browse/sugaku/7/0/_contents/-char/ja/ … にあります。問題のpdfファイルを開いて問題12を見てください。そこに歴史的な予想の原型が書いてあります。
@genkuroki #数学 訂正https://twitter.com/genkuroki/status/671255698009923584 …の「(π/2)」を「(2/π)」に訂正します。分子分母がひっくり返っていた。こういう自明な誤りはよくある。
@genkuroki #掛算 #数学 数学ミステリー白熱教室第3回の終わりの方でエドワード・フレンケルさんが重要な人物の1人として名を挙げている志村五郎さんは http://blog.goo.ne.jp/mh0920-yh/e/571d15ca3834e78975c73c4f3e083a6b … に登場する志村五郎さんと同一人物です。



